Recent Advances in Efficient and Scalable Graph Neural Networks
An overview of papers on efficient Graph Neural Networks and scalable Graph Representation Learning for real-world applications.
 Photo by Jake Givens
Photo by Jake Givensawesome-efficient-gnns.🚀 Efficient Graph Neural Networks
This article aims to provide an overview of key ideas on efficient Graph Neural Networks and scalable Graph Representation Learning. We will cover key developments in data preparation, GNN architectures, and learning paradigms that are enabling Graph Neural Networks to scale to real-world graphs and real-time applications.
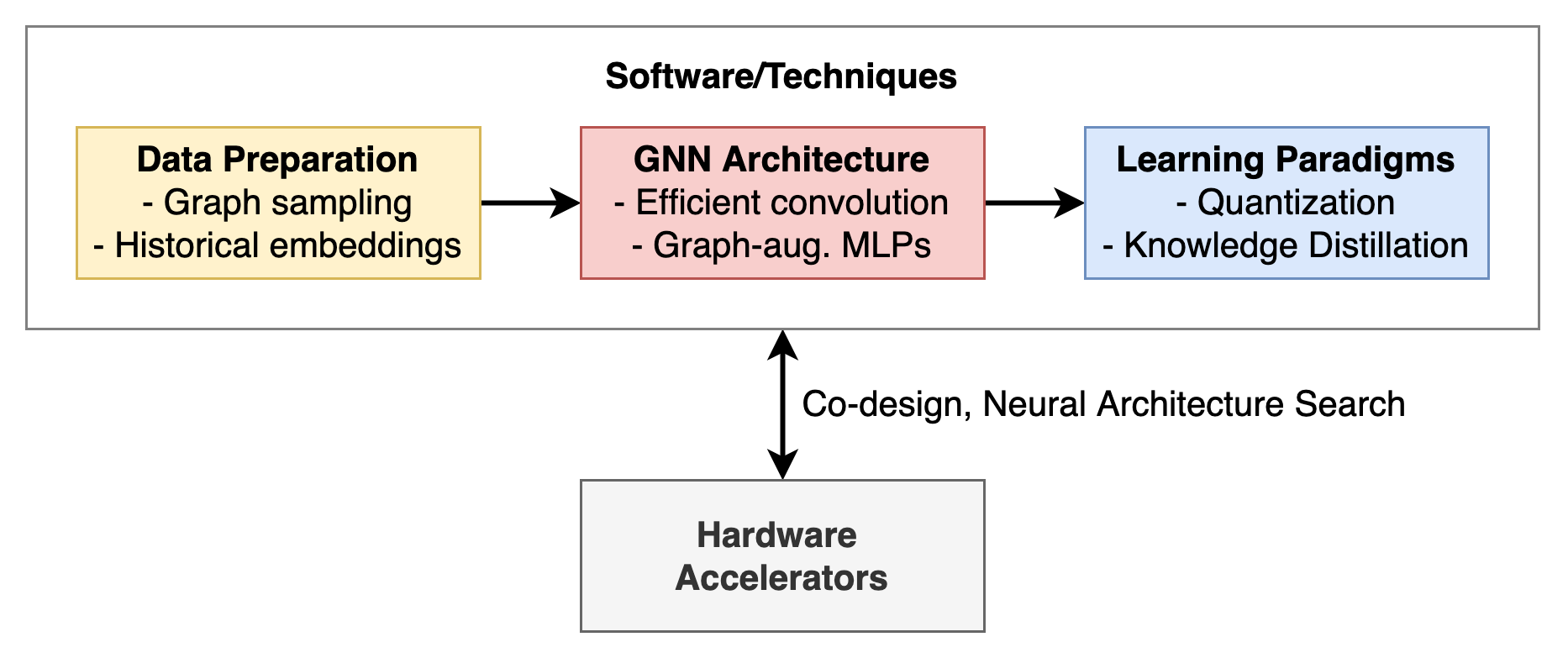
Table of Contents
Real-world Challenges for Graph Neural Networks
Graph Neural Networks are an emerging line of deep learning architectures that can build actionable representations of irregular data structures such as graphs, sets, and 3D point clouds. In recent years, GNNs have powered several impactful applications in fields ranging from social networks and recomendation systems to biomedical discovery and traffic forecasting.
Building GNNs to handle real-world graph data poses several theoretical and engineering challenges, the most prominent among which are:
1. Giant Graphs – Memory Limitations
Real-world networks can grow ginormously large and complex. As an illustration, Facebook has almost 3 Billion active accounts, which correspond to graph nodes, and these accounts are interacting with each other in a myriad of ways (liking, commenting, sharing, etc.), creating bajillions of graph edges. Imagine trying to train a GNN on such a network – how to even fit giant graphs into GPU memory and perform gradient descent to train the parameters without running into scalability issues?
2. Sparse Computations – Hardware Limitations
Graphs are inherently sparse objects, and GNNs should ideally leverage their sparsity for efficient and scalable computation. This is easier said than done, as modern GPUs are designed to handle dense operations on matrices. While customized hardware accelerators for sparse matrices could significantly boost the latency and scalability of GNNs, their design remains an open question.

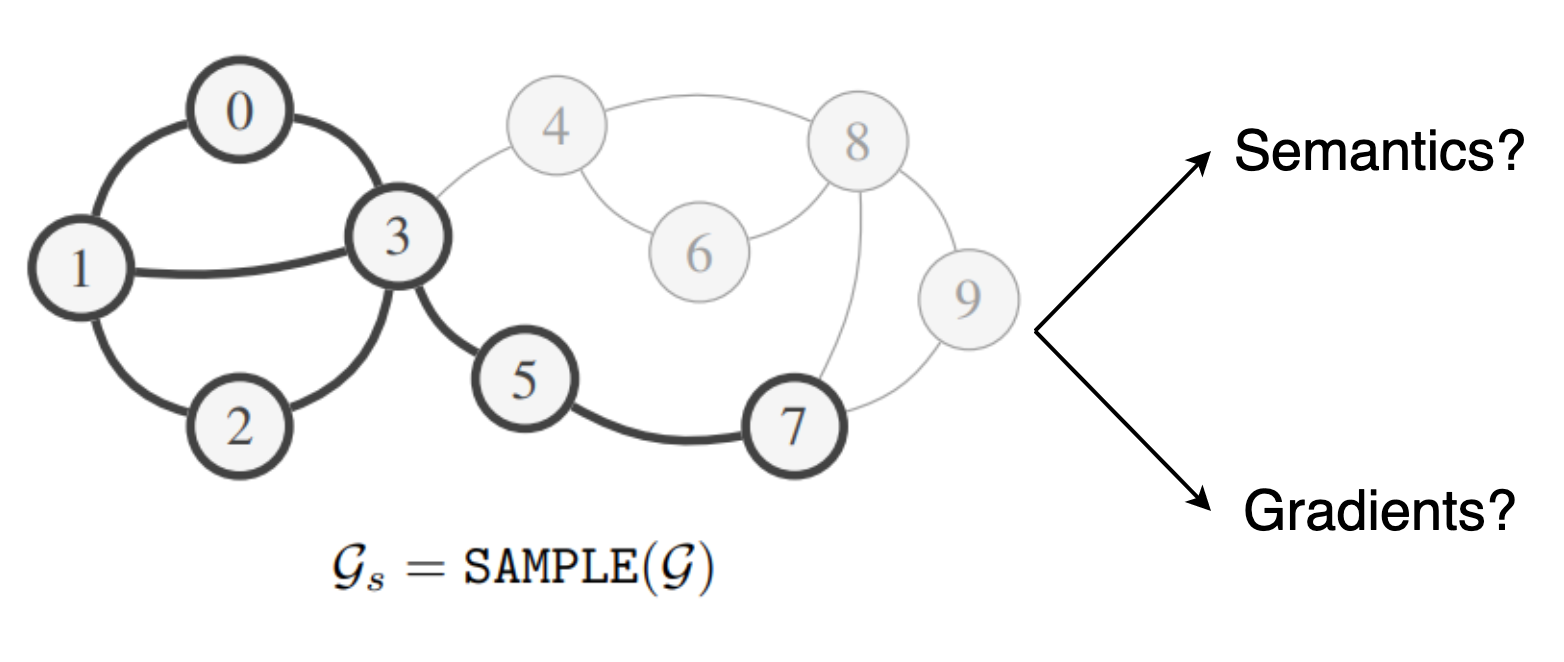
3. Graph Subsampling – Reliability Limitations
One straightforward approach for dealing with giant graphs is to split them into smaller subgraphs and train GNNs via mini-batched gradient descent (each subgraph could be a mini-batch). However, there are major issues with this approach: Unlike standard datasets for machine learning where samples are statistically independent, the relational structure of network data creates a statistical dependence between samples. Thus, it is not straightforward to ensure that the subgraphs retain the semantics of the full graph, as well as provide reliable gradients for training GNNs.
Handling Large-scale Graphs
Graph Subsampling Techniques
The first line of papers attempting to scale GNNs to giant graphs looked at graph subsampling to split large graphs into manageable subgraphs. ClusterGCN leveraged clustering algorithms to split the graph into clustered subgraphs and trained GNNs on by using each cluster as a mini-batch. This works well enough in practice, especially for homophillous graphs where clusters generally form meaniningful communities with similar labels.
[KDD 2019] Cluster-GCN: An Efficient Algorithm for Training Deep and Large Graph Convolutional Networks. Wei-Lin Chiang, Xuanqing Liu, Si Si, Yang Li, Samy Bengio, Cho-Jui Hsieh.
GraphSAINT proposed a more general probabilistic graph sampler to construct mini-batches of subgraphs. Possible sampling schemes included uniform node/edge sampling as well as random-walk sampling. However, subsampling approaches may limit the performance of models compared to training on the full graph due to the reliability issues highlighted in the previous section (semantics as well as gradient information).
[ICLR 2020] GraphSAINT: Graph Sampling Based Inductive Learning Method. Hanqing Zeng, Hongkuan Zhou, Ajitesh Srivastava, Rajgopal Kannan, Viktor Prasanna.
Historical Node Embeddings
GNNAutoScale (GAS) is a promising recent alternative to basic subsampling techniques for scaling GNNs to large graphs. GAS builds upon previous work by Chen et al. on Historical Node Embeddings, i.e. re-using node embeddings from previous training epochs for the current epoch.
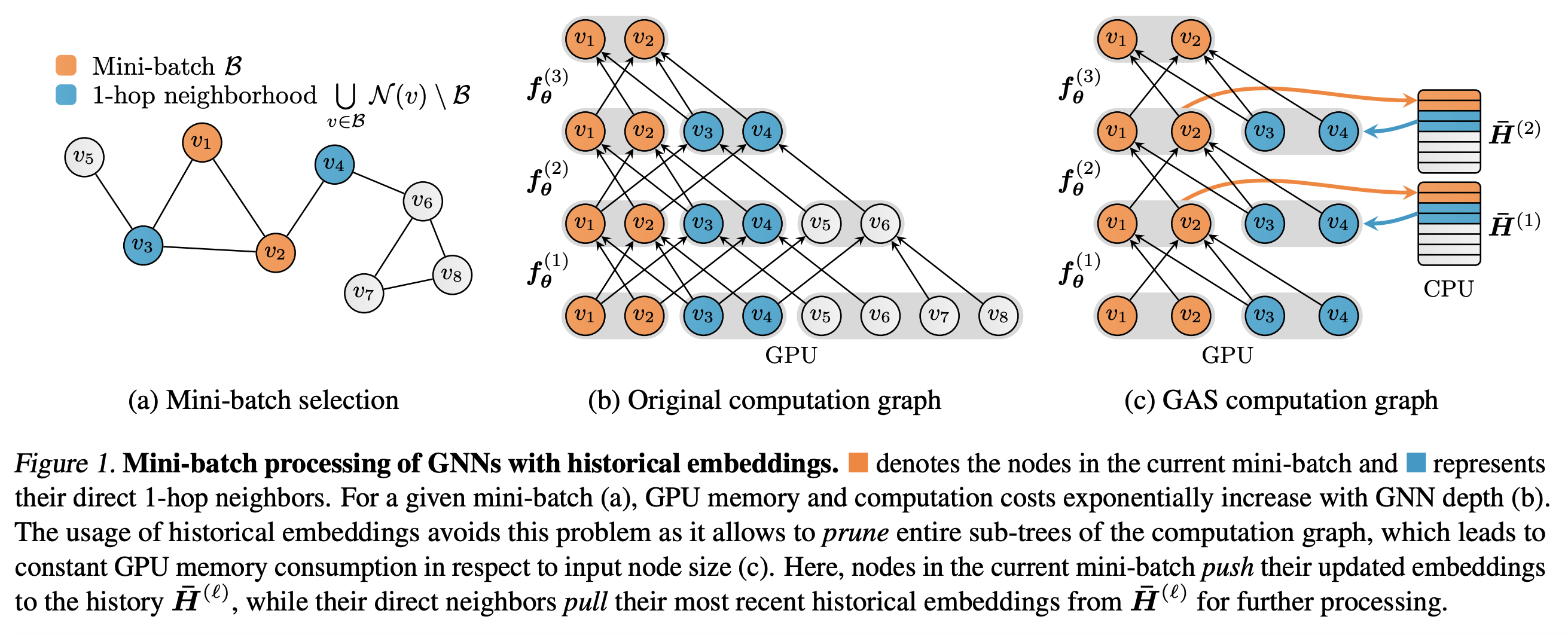
There are two major components to the GAS framework: Firstly, they build a mini-batch of nodes (they perform fast random subsampling) and prune the GNN computational graph to only retain nodes inside the mini-batch and their 1-hop neighbors – this implies that GAS scales independent of GNN depth. Secondly, whenever the GNN aggregation requires out-of-mini-batch node embeddings, GAS retreives them from historical embeddings stored on the CPU. The historical embeddings of current mini-batch nodes are also constantly updated.
This second part is the key difference from subsampling – it enables GNNs to be maximally expressive and utilize full neighborhood information via a combination of mini-batch and historical embeddings, while ensuring scalability to very large graphs.
The authors of GAS have also integrated their idea into the popular PyTorch Geometric library. This enables the training of most message-passing GNNs on very large graphs while reducing their GPU memory requirement and retaining close to full-batch performance (i.e. performance when training on the full graph).
[ICML 2018] Stochastic Training of Graph Convolutional Networks with Variance Reduction Jianfei Chen, Jun Zhu, Le Song.
[ICML 2021] GNNAutoScale: Scalable and Expressive Graph Neural Networks via Historical Embeddings. Matthias Fey, Jan E. Lenssen, Frank Weichert, Jure Leskovec.
Some other ideas in the toolkit for scaling to large graphs include:
[CVPR 2020] L2-GCN: Layer-Wise and Learned Efficient Training of Graph Convolutional Networks. Yuning You, Tianlong Chen, Zhangyang Wang, Yang Shen.
[KDD 2020] Scaling Graph Neural Networks with Approximate PageRank. Aleksandar Bojchevski, Johannes Klicpera, Bryan Perozzi, Amol Kapoor, Martin Blais, Benedek Rózemberczki, Michal Lukasik, Stephan Günnemann.
[ICLR 2021] Graph Traversal with Tensor Functionals: A Meta-Algorithm for Scalable Learning. Elan Markowitz, Keshav Balasubramanian, Mehrnoosh Mirtaheri, Sami Abu-El-Haija, Bryan Perozzi, Greg Ver Steeg, Aram Galstyan.
[NeurIPS 2021] Decoupling the Depth and Scope of Graph Neural Networks. Hanqing Zeng, Muhan Zhang, Yinglong Xia, Ajitesh Srivastava, Andrey Malevich, Rajgopal Kannan, Viktor Prasanna, Long Jin, Ren Chen.
Scalable and Resource-efficient GNN Architectures
Graph-augmented MLPs
Here is a counter-intuitive idea for developing scalable GNNs: just run simple MLPs on mini-batches of nodes without accounting for the relational structure of the graph!
Simplifying Graph Convolutional Networks (SGC) by Wu et al. was the first to propose this idea. SGC essentially ‘deconstructs’ the vanilla GCN by Kipf and Welling by decoupling the (expensive but non-learnt) sparse neighborhood feature aggregation step from the (inexpensive and learnable) linear projection followed by ReLU non-linearity step. For large graphs, feature aggregation can be pre-computed efficiently on CPUs (CPUs are decent at handling sparse operations) and the ‘structure-augmented’ node features can then be batched and passed to an MLP which is trained on the GPU.
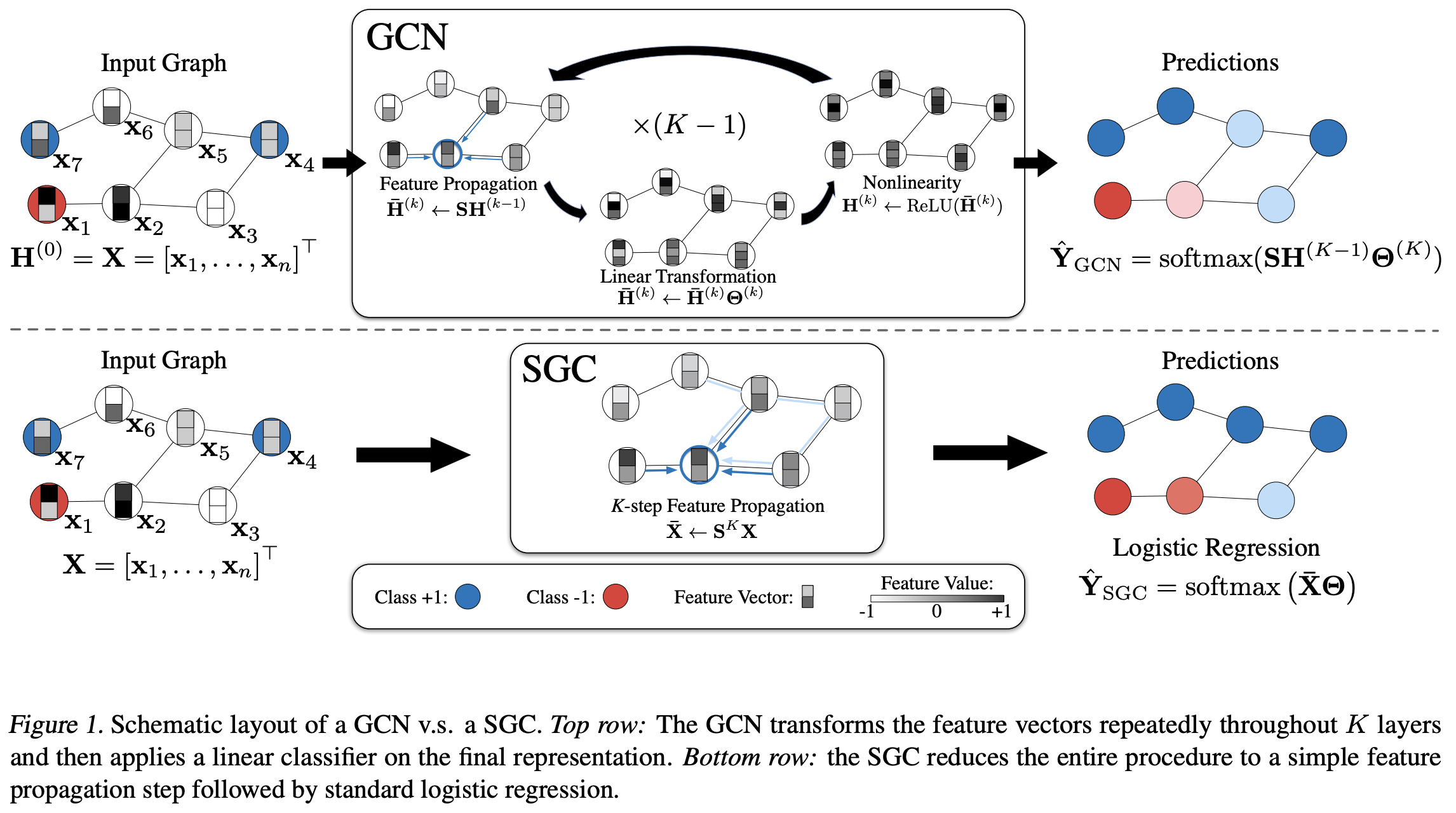
[ICML 2019] Simplifying Graph Convolutional Networks. Felix Wu, Tianyi Zhang, Amauri Holanda de Souza Jr., Christopher Fifty, Tao Yu, Kilian Q. Weinberger.
SIGN: Scalable Inception Graph Neural Networks by Rossi et al. tries to take the SGC idea one step further by seeking inspiration from Inception networks for computer vision and running multiple pre-computation steps to obtain better initial structural features for each graph node.
[ICML 2020 Workshop] SIGN: Scalable Inception Graph Neural Networks. Fabrizio Frasca, Emanuele Rossi, Davide Eynard, Ben Chamberlain, Michael Bronstein, Federico Monti.
Other interesting developments in this line of architectures includes Chen et al.’s work exploring the theoretical limitations of structure-augmented MLPs, as well as Huang et al.’s paper showing that a similar label propogation approach after running MLPs on node features outperforms more cumbersome GNNs on homophillous graphs.
[ICLR 2021] On Graph Neural Networks versus Graph-Augmented MLPs. Lei Chen, Zhengdao Chen, Joan Bruna.
[ICLR 2021] Combining Label Propagation and Simple Models Out-performs Graph Neural Networks. Qian Huang, Horace He, Abhay Singh, Ser-Nam Lim, Austin R. Benson
Efficient Graph Convolutional Layers
Unfortunately, many tasks beyond node classification on homophillous graphs may require significantly more expressive GNN architectures than SGC/SIGN-like models. This is usually the case for graph-level classication and reasoning tasks where top performing GNNs generally utilize features over both nodes and edges.
Such models follow the message-passing flavor of GNN architecture design (as popularized by Petar Veličković) and can be considered ‘anisotropic’ in that they treat each edge distinctly (whereas vanilla GCNs are ‘isotropic’ in that the same learnable weights are applied to each edge). However, maintaining hidden embeddings over nodes as well as edges in each layer significantly increases both the inference latency and memory requirements of GNNs.
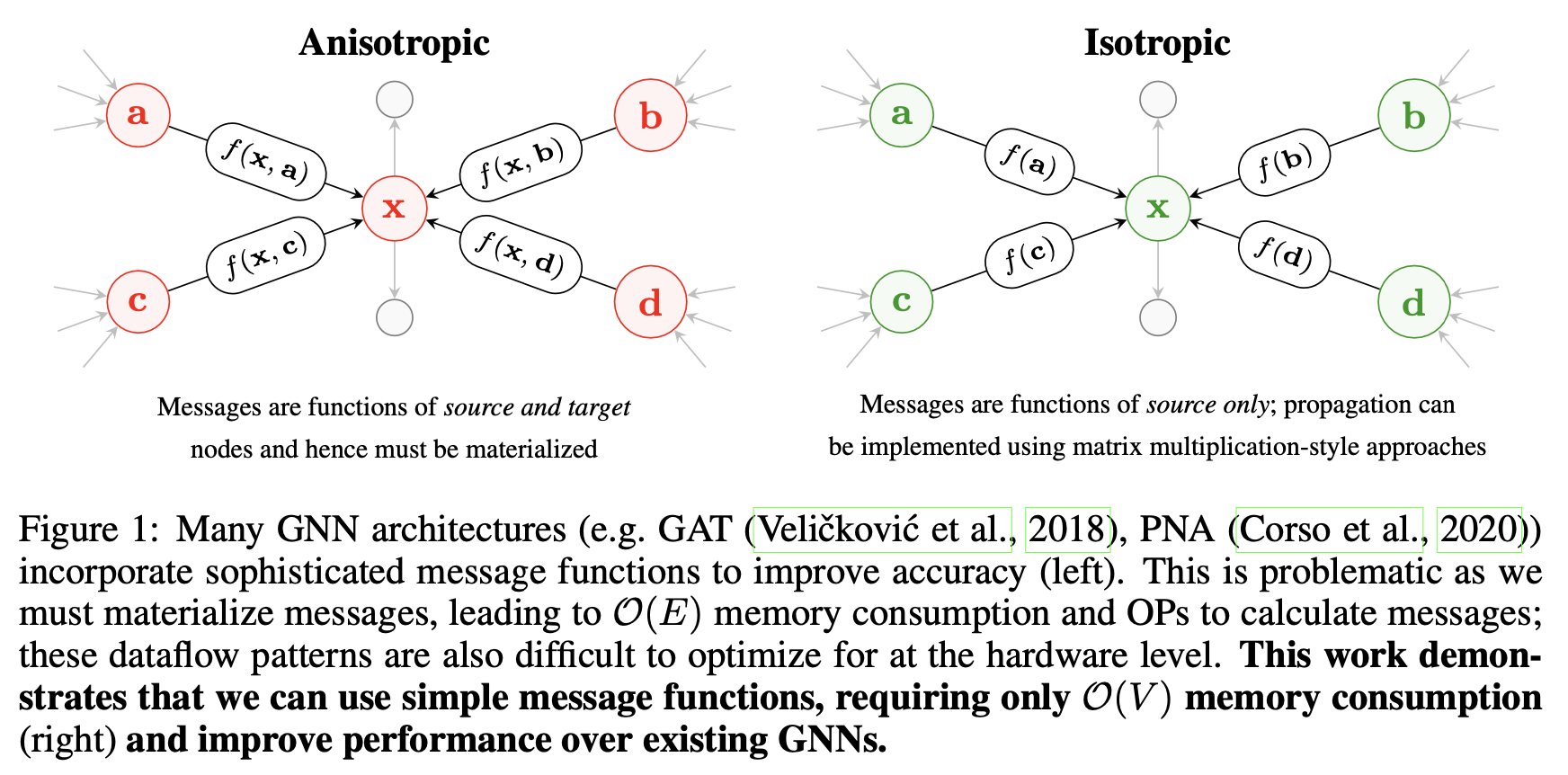
Efficient Graph Convolution (EGC) by Tailor et al. tries to resolve this dilemna. They start with the basic GCN design (which is decently scalable for batches of medium sized graphs) and design a maximally expressive version of convolutional GNNs that retains the scalability of GCNs. Impressively, they outperform more complex and cumbersome baselines across graph classification tasks from the Open Graph Benchmark.
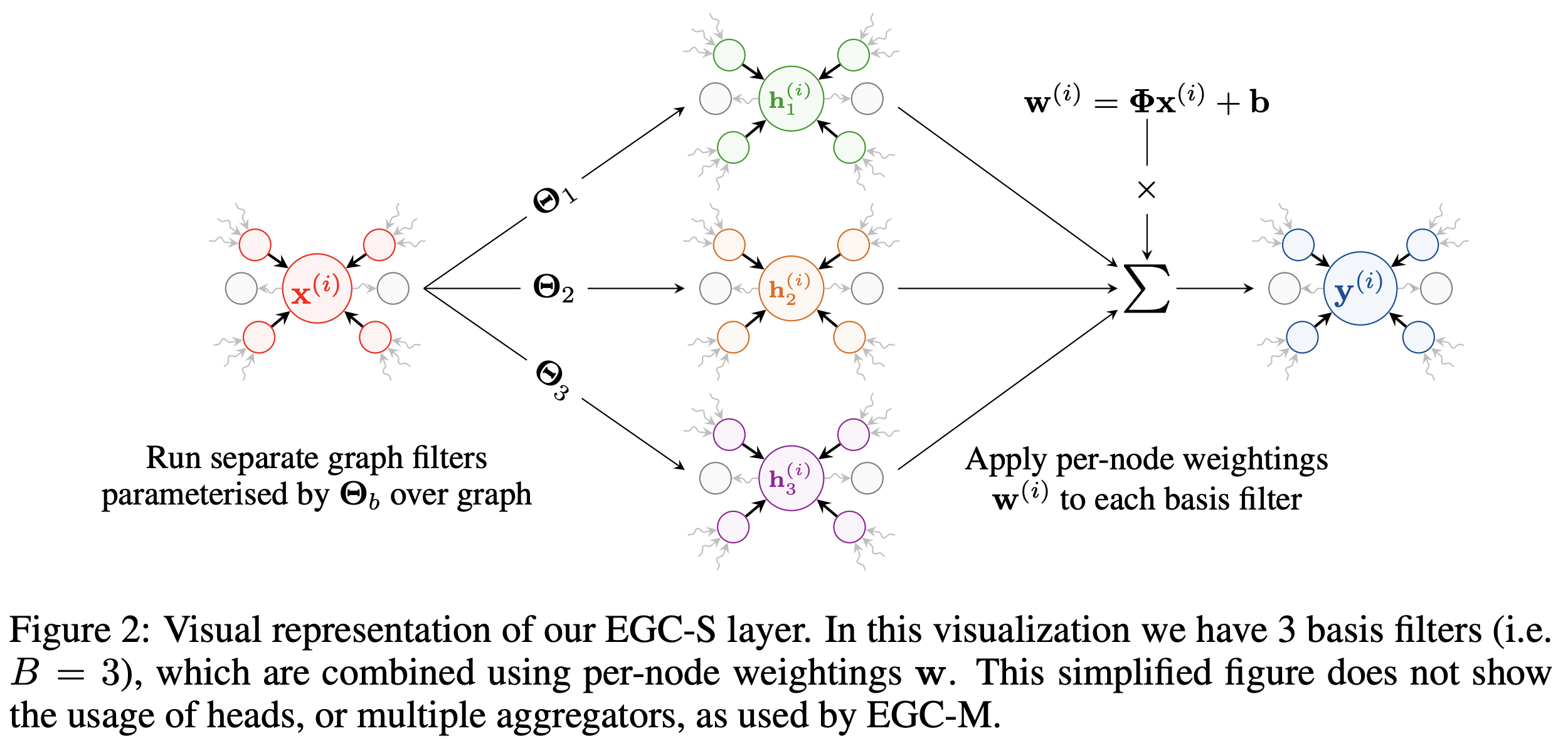
The EGC layer has also been integrated into PyTorch Geometric and can be a plug-and-play replacement for improving your GNN’s performance and scalability.
[ICLR 2022] Do We Need Anisotropic Graph Neural Networks?. Shyam A. Tailor, Felix L. Opolka, Pietro Liò, Nicholas D. Lane.
Another interesting idea from Li et al. leverages advances from efficient ConvNets in computer vision (reversible connections, group convolutions, weight tying, and equilibrium models) to boost the memory and parameter efficiency of GNNs. Their framework enables the training of GNNs with (an unprescedented) 1000+ layers and strong performance across large-scale node classification tasks from the Open Graph Benchmark.
[ICML 2021] Training Graph Neural Networks with 1000 Layers. Guohao Li, Matthias Müller, Bernard Ghanem, Vladlen Koltun.
Learning Paradigms for GNN Compression
Beyond data preparation techniques and efficient model architectures, the learning papradigm, i.e. the way that the model is trained, can also significantly boost the performance and latency of GNNs.
Knowledge Distillation for Boosting Performance
Knowledge Distillation (KD) is a generic neural network learning paradigm that transfers knowledge from high performance but resource-intensive teacher models to resource-efficient students. Pioneered by Hinton et al., KD trains the student to match the output logits of teacher models in addition to standard supervised learning losses.
Recent work by Yang et al. and, subsequently, Zhang et al., have shown how powerful this simple logit-based KD idea can be for developing resource-efficient GNNs: They train expressive GNNs as teacher models and use KD to transfer knowledge to MLP students for much easier deployment when the node features and graph structure are highly correlated. This idea may be extended to graph-augmented MLPs like SGC or SIGN from the previous section, significantly boosting the performance of MLP-like models while being easy to deploy in production systems.
[WWW 2021] Extract the Knowledge of Graph Neural Networks and Go Beyond it: An Effective Knowledge Distillation Framework. Cheng Yang, Jiawei Liu, Chuan Shi.
[ICLR 2022] Graph-less Neural Networks: Teaching Old MLPs New Tricks via Distillation. Shichang Zhang, Yozen Liu, Yizhou Sun, Neil Shah.
In computer vision, practioners have attempted to go beyond logit-based KD by transferring representational knowledge from the teacher to the student through loss functions that align their latent embedding spaces.
Yang et al.’s pioneering work first explored representation distillation for GNNs by training the student to preserve local topology from the teacher’s node embedding space. They termed this approach Local Structure Preservation (LSP), as it encourage the student to mimic the pairwise similarities with immediate neighbours present in the teacher’s node embedding space.
Joshi et al. recently extended the LSP study to consider global topological structure by preserving latent interactions beyond immediate neighbors. They propose two new representation distillation objectives for GNNs: (1) An explicit approach – Global Structure Preservation, which extends LSP to consider all pairwise similarities; and (2) An implicit approach – Graph Contrastive Representation Distillation, which uses contrastive learning to align the student node embeddings to those of the teacher in a shared representation space.
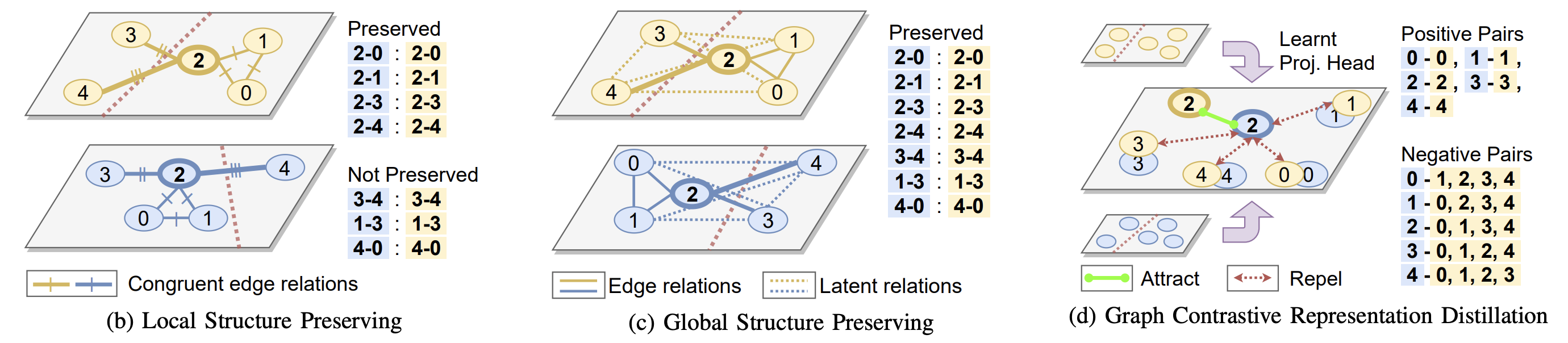
Joshi et al.’s experiments on Open Graph Benchmark datasets show that training lightweight GNNs with representation distillation significantly boosts their empirical performance as well as robustness to noisy or out-of-distribution data.
[CVPR 2020] Distilling Knowledge from Graph Convolutional Networks. Yiding Yang, Jiayan Qiu, Mingli Song, Dacheng Tao, Xinchao Wang.
[ArXiv 2021] On Representation Knowledge Distillation for Graph Neural Networks. Chaitanya K. Joshi, Fayao Liu, Xu Xun, Jie Lin, Chuan-Sheng Foo.
Some other approaches to KD for GNNs include teacher-free distillation, a.k.a. self-distillation, as well as data-free distillation.
[IJCAI 2021] On Self-Distilling Graph Neural Network. Yuzhao Chen, Yatao Bian, Xi Xiao, Yu Rong, Tingyang Xu, Junzhou Huang.
[IJCAI 2021] Graph-Free Knowledge Distillation for Graph Neural Networks. Xiang Deng, Zhongfei Zhang.
Quantization for Low Precision GNNs
Quantization Aware Training (QAT) is another generic neural network learning paradigm.
While conventional neural network model weights and activations are stored as 32-bit floating point numbers FP32, QAT trains models with lower precision, integer weights and activations such as INT8 or INT4.
Low precision models enjoy significant gains in inference latency, albeit at the cost of reduced performance.
DegreeQuant by Tailor et al. proposes a QAT technique specialized for GNNs.
Generic QAT, which was designed for CNNs for computer vision, can often lead to very poor performance after quantization when applied to GNNs.
DegreeQuant aims to alleviate this by smartly incorporating the graph structure of the underlying data into the quantization procedure:
They show that nodes with many neighbours (high degree) can lead to instability during QAT, and propose to stochastically mask high degree nodes when performing QAT.
This enables more stable QAT for GNNs and minimizes performance reductions at INT8 compared to the FP32 model.
[ICLR 2021] Degree-Quant: Quantization-Aware Training for Graph Neural Networks. Shyam A. Tailor, Javier Fernandez-Marques, Nicholas D. Lane.
Other ideas for quantizing GNNs include leveraging Neural Architecture Search by Zhao et al., and binarization by Bahri et al. (which is an extreme case of quantization). In general, some of the performance reduction from QAT can be gained back via Knowledge Distillation, as shown in Bahri et al.’s as well as in Joshi et al.’s Graph Contrastive Representation Distillation paper from the previous section.
[EuroMLSys 2021] Learned Low Precision Graph Neural Networks. Yiren Zhao, Duo Wang, Daniel Bates, Robert Mullins, Mateja Jamnik, Pietro Lio.
[CVPR 2021] Binary Graph Neural Networks. Mehdi Bahri, Gaétan Bahl, Stefanos Zafeiriou.
Conclusion and Outlook
This article focused on efficient Graph Neural Networks and scalable Graph Representation Learning. We started by identifying the theoretical and engineering challenges with real-world GNNs:
- Giant Graphs – Memory Limitations
- Sparse Computations – Hardware Limitations
- Graph Subsampling – Reliability Limitations
We then introduced three key ideas which may form the toolbox for developing efficient and scalable GNNs:
- Data Preparation - From sampling large-scale graphs to CPU-GPU hybrid training via historical node embedding lookups.
- Efficient Architectures - Graph-augmented MLPs for scaling to giant networks, and efficient graph convolution designs for real-time inference on batches of graph data.
- Learning Paradigms - Combining Quantization Aware Training (low precision model weights and activations) with Knowledge Distillation (improving efficient GNNs using expressive teacher models) for maximizing inference latency as well as performance.

In the near future, we expect the research community to continue to advance and mature the GNN efficiency and scalability toolbox, potentially via direct integration into GNN libraries such as PyTorch Geometric and DGL. We also expect to hear more and more success stories of GNNs handling real-world graphs and real-time applications.
In the long run, we hope that graph data + GNNs transition from an esoteric and emerging research field to a standard data + model format for machine learning research as well as applications (much like 2D images + CNNs, or text + Transformers). As a result, we may expect to see deeper integration of GNNs into standard frameworks such as PyTorch or TensorFlow, the development of specialized hardware accelerators for GNNs, as well as more sophisticated hardware-software co-design for graph data.
Indeed, these efforts may already be taking place within companies which are deriving great business value from graph data and GNNs!
Comprehensive Surveys
For more in-depth coverage into the topics covered in this article, please refer to the following surveys.
Abadal et al.’s extensive survey covers everything from the funadamentals of GNNs to the design of hardware accelerators for graph representation learning (something that this article does not go into).
[ACM Computing 2021] Computing Graph Neural Networks: A Survey from Algorithms to Accelerators. Sergi Abadal, Akshay Jain, Robert Guirado, Jorge López-Alonso, Eduard Alarcón.
Zhang et al. focus on Neural Architecture Search and AutoML for GNNs. AutoML techniques could play a key role in hardware-software co-design by identifying lightweight and high performing GNN architectures. (NAS is another topic that this article skips.) They also released an accompanying toolkit on GitHub for benchmarking Graph AutoML.
[IJCAI 2021] Automated Machine Learning on Graphs: A Survey. Ziwei Zhang, Xin Wang, Wenwu Zhu.
Liu et al.’s recent survey does a deep dive into many of the topics this article discusses: graph sampling, graph sparsification, efficient GNN architectures, and GNN compression. This survey provides a systematic taxonomy of the efficient GNNs toolbox and also points to several exciting directions to stimulate future research. The same team also had a previous survey which focuses on graph subsampling.
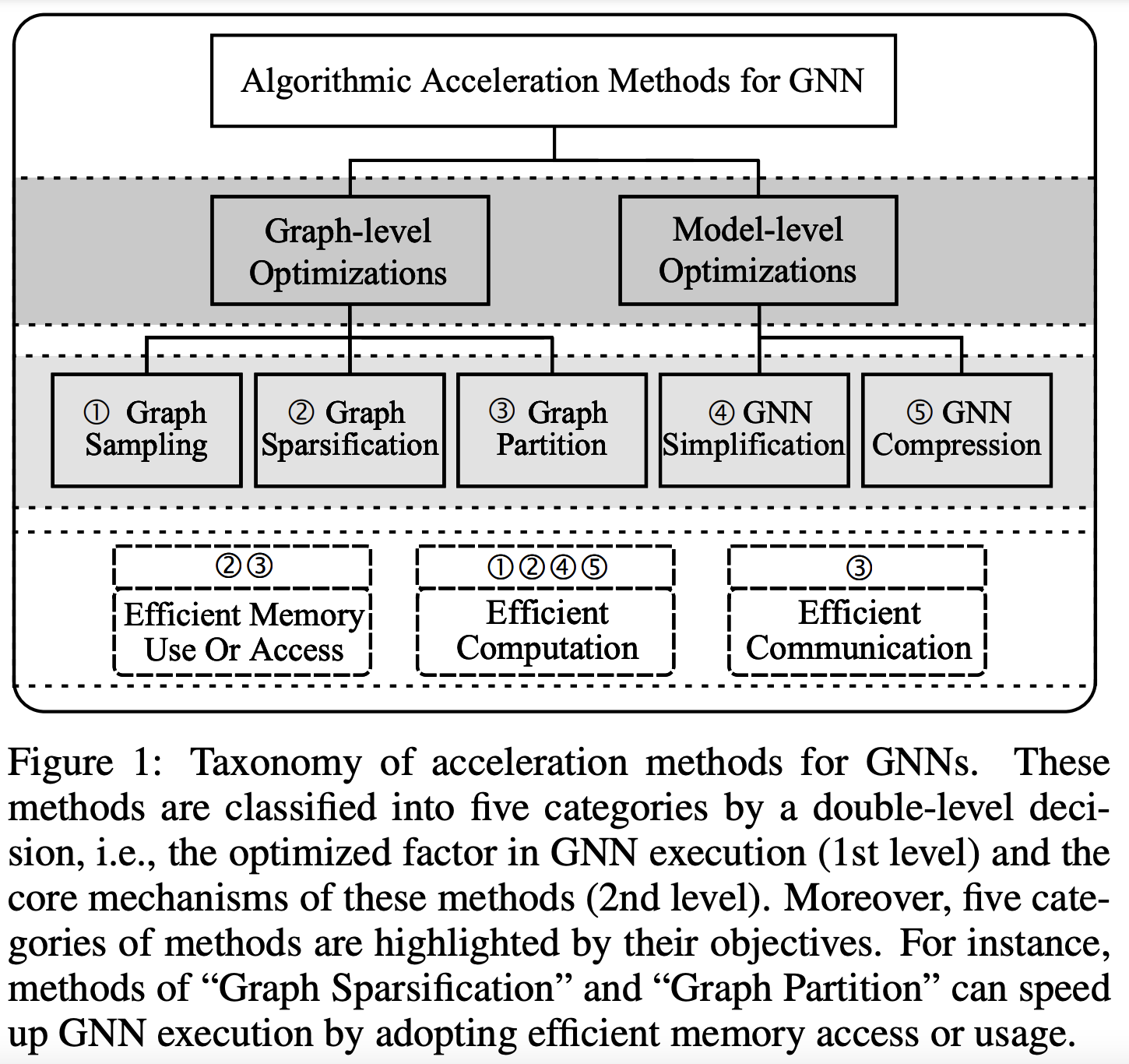
[ArXiv 2022] Survey on Graph Neural Network Acceleration: An Algorithmic Perspective. Xin Liu, Mingyu Yan, Lei Deng, Guoqi Li, Xiaochun Ye, Dongrui Fan, Shirui Pan, Yuan Xie.
[ArXiv 2021] Sampling methods for efficient training of graph convolutional networks: A survey. Xin Liu, Mingyu Yan, Lei Deng, Guoqi Li, Xiaochun Ye, Dongrui Fan.
Please reach out via email for any missing references, comments, or feedback.
Citation: For attribution in academic contexts, please cite this work as:
@article{joshi2022efficientgnns,
author = {Joshi, Chaitanya K.},
title = {Recent Advances in Efficient and Scalable Graph Neural Networks},
year = {2022},
howpublished = {\url{https://www.chaitjo.com/post/efficient-gnns/}},
}
Acknowledgements: We would like to thank Shyam Tailor, Hanqing Zeng, Liu Xin, Shichang Zhang, and Neil Shah for helpful feedback and discussions.