Neural Combinatorial Optimization

Operations Research and Combinatorial Problems

Operations Research (OR) started in the first world war as an initiative to use mathematics and computer science to assist military planners in their decisions. Nowadays it is widely used in the industry, including but not limited to transportation, supply chain, energy, finance, and scheduling.

OR Problems are formulated as integer constrained optimization, i.e., with integral or binary variables (called decision variables). While not all such problems are hard to solve (e.g., finding the shortest path between two locations), we concentrate on Combinatorial (NP-Hard) problems. NP-Hard problems are impossible to solve optimally at large scales as exhaustively searching for their solutions is beyond the limits of modern computers. The Travelling Salesman Problem (TSP) and the Minimum Spanning Tree Problem (MST) are two of the most popular examples for such problems defined using graphs.

Robust approximation algorithms to popular problems have immense practical applications and are the backbone of modern industries.

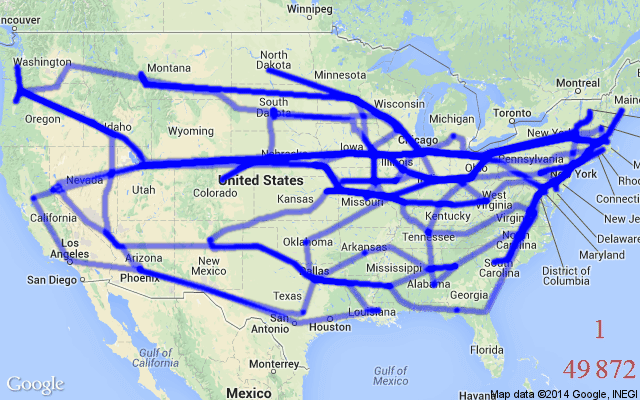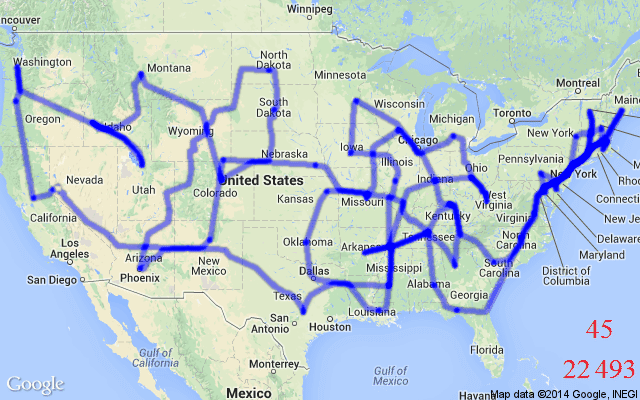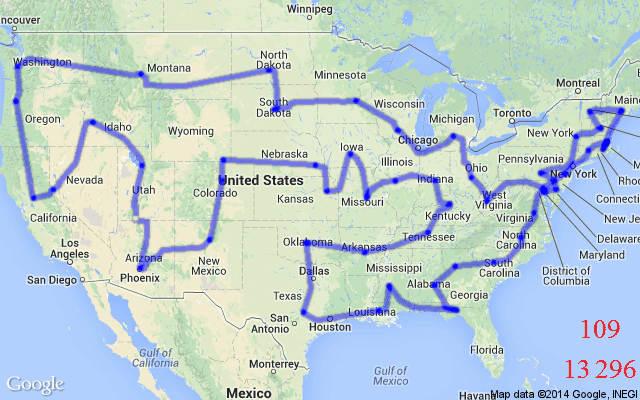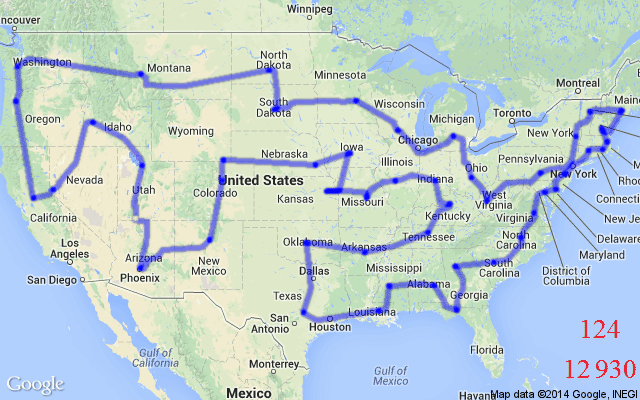
Neural Combinatorial Optimization

Although handcrafted heuristic algorithms are able to solve problems such as TSP with up to a million variables, designing good heuristics often requires significant specialized knowledge and years of trial-and-error. The state-of-the-art TSP solver, Concorde, leverages over 50 years of research on linear programming, cutting plane algorithms and branch-and-bound. Concorde can find optimal solutions up to tens of thousands of nodes, but with extremely long execution time.

At our lab, we’re working on automating and augmenting such expert intuition through Machine Learning [Bengio et al., 2018].

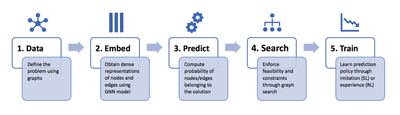
Since most problems are highly structured, heuristics take the form of rules or policies to make sequential decisions, e.g., determine the TSP tour one city at a time. Our research uses deep neural networks to parameterize these policies and train them directly from problem instances. In particular, Graph Neural Networks are the perfect fit for the task because they naturally operate on the graph structure of these problems.Once trained, approximate GNN-based solvers have significantly favorable time complexity than their OR counterparts, making them highly desirable for real-time decision-making problems, such as routing problems.

Why TSP in particular?

I’ve been working on end-to-end learning for combinatorial problems, specifically TSP, since my Bachelor’s Thesis with Prof. Xavier Bresson. Since then, I’ve travelled to my first real conferences based on this work: I gave an invited talk at an INFORMS 2019 session. Then, I went to the promised land: NeurIPS! I presented a workshop paper at the Graph Representation Learning workshop. XB also organized an exciting workshop at IPAM titled “Deep Learning and Combinatorial Optimization”.

So, why am I excited to study TSP, in particular?

(1) The problem has an amazing history of serving as an engine of discovery for applied mathematics, with several legendary computer scientists and mathematicians having a crack at it. Here’s an amazing talk by William Cook, the co-inventor of the current state-of-the-art Concorde TSP solver.

(2) TSP has been the focus of intense research in the combinatorial optimization community. If you come up with a new solver, e.g., a learning-based solver, you need to benchmark it on TSP. TSP’s multi-scale nature makes it a challenging graph task which requires reasoning about both local node neighborhoods as well as global graph structure.

(3) Learning-based approaches to TSP have the potential to be a breakthrough for OR if they are able to firstly learn efficient heuristics on small scale problems and then generalize robustly to larger instances. However, such scale-invariant generalization in deep learning is fleeting, not just for TSP, but as a general unsolved challenge. Building systems that can generalize and interpolate beyond training data is the most exciting prospect for me! Update: We explore this in our latest paper.

At the same time, the more profound motivation of using deep learning for combinatorial optimization is not to outperform non-learned, specialized approaches on well-studied problems. Neural networks can be used as a general tool for tackling previously un-encountered NP-hard problems, especially those that are non-trivial to design heuristics for [Bello et al., 2016]. I’m super excited about recent applications of neural combinatorial optimization for accelarating drug discovery, optimizing operating systems and designing computer chips.