Abstract
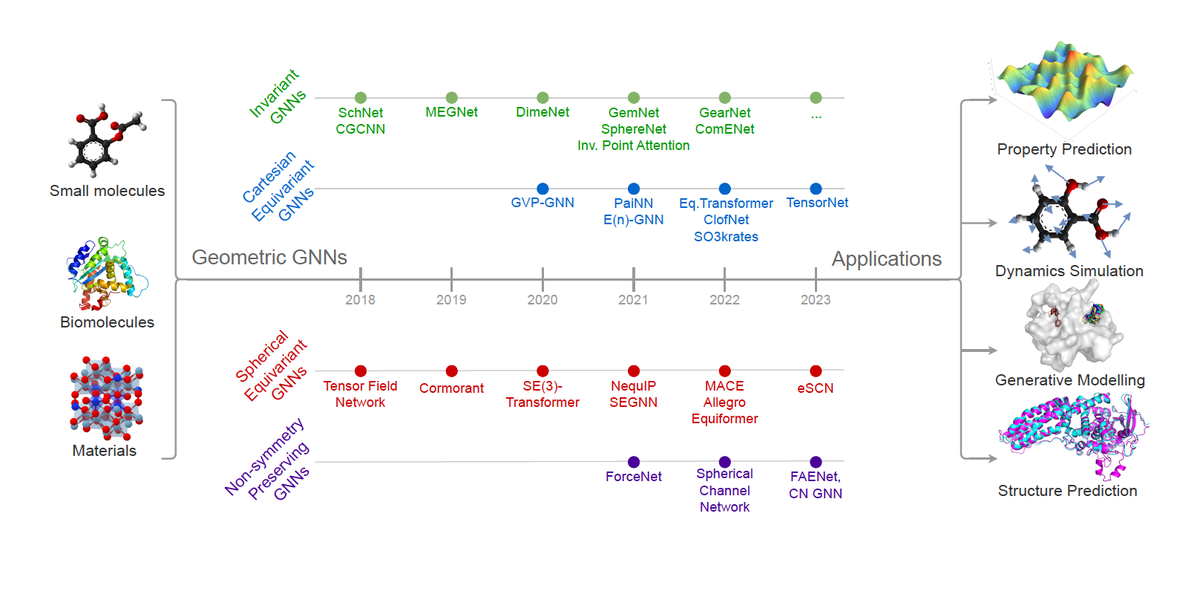
Recent advances in computational modelling of atomic systems, spanning molecules, proteins, and materials, represent them as geometric graphs with atoms embedded as nodes in 3D Euclidean space. In these graphs, the geometric attributes transform according to the inherent physical symmetries of 3D atomic systems, including rotations and translations in Euclidean space, as well as node permutations. In recent years, Geometric Graph Neural Networks have emerged as the preferred machine learning architecture powering applications ranging from protein structure prediction to molecular simulations and material generation. Their specificity lies in the inductive biases they leverage – such as physical symmetries and chemical properties – to learn informative representations of these geometric graphs. In this opinionated paper, we provide a comprehensive and self-contained overview of the field of Geometric GNNs for 3D atomic systems. We cover fundamental background material and introduce a pedagogical taxonomy of Geometric GNN architectures:(1) invariant networks, (2) equivariant networks in Cartesian basis, (3) equivariant networks in spherical basis, and (4) unconstrained networks. Additionally, we outline key datasets and application areas and suggest future research directions. The objective of this work is to present a structured perspective on the field, making it accessible to newcomers and aiding practitioners in gaining an intuition for its mathematical abstractions.